Cellular automata were studied in the early 1950s as a possible model for biological systems (Wolfram 2002, p. 48). Comprehensive studies of cellular automata have been performed by S. Wolfram starting in the 1980s, and Wolfram's fundamental research in the field culminated in the publication of his book A New Kind of Science (Wolfram 2002) in which Wolfram presents a gigantic collection of results concerning automata, among which are a number of groundbreaking new discoveries.
The Season 2 episode "Bettor or Worse" (2006) of the television crime drama NUMB3RS mentions one-dimensional cellular automata.Cellular automata come in a variety of shapes and varieties. One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. The simplest such "grid" is a one-dimensional line.
In two dimensions, square, triangular, and hexagonal grids may be considered. Cellular automata may also be constructed on Cartesian grids in arbitrary numbers of dimensions, with the -dimensional integer lattice being the most common choice. Cellular automata on a -dimensional integer lattice are implemented in Mathematica as CellularAutomaton[rule, init, steps].
The number of colors (or distinct states) a cellular automaton may assume must also be specified. This number is typically an integer, with (binary) being the simplest choice. For a binary automaton, color 0 is commonly called "white," and color 1 is commonly called "black". However, cellular automata having a continuous range of possible values may also be considered.
In addition to the grid on which a cellular automaton lives and the colors its cells may assume, the neighborhood over which cells affect one another must also be specified. The simplest choice is "nearest neighbors," in which only cells directly adjacent to a given cell may be affected at each time step. Two common neighborhoods in the case of a two-dimensional cellular automaton on a square grid are the so-called Moore neighborhood (a square neighborhood) and the von Neumann neighborhood (a diamond-shaped neighborhood).
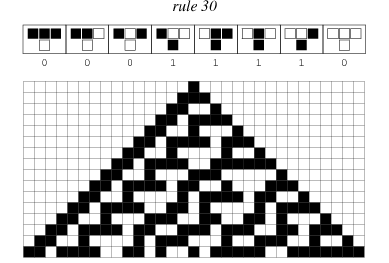
The simplest type of cellular automaton is a binary, nearest-neighbor, one-dimensional automaton. Such automata were called "elementary cellular automata" by S. Wolfram, who has extensively studied their amazing properties (Wolfram 1983; 2002, p. 57). There are 256 such automata, each of which can be indexed by a unique binary number whose decimal representation is known as the "rule" for the particular automaton. An illustration of rule 30 is shown above together with the evolution it produces after 15 steps starting from a single black cell.