Cellular Automata

Cellular automata are simulations on a linear, square, or cubic grid on which each cell can be in a single state, often just ON and OFF, and where each cell operates on its own, taking the states of its neighbors as input and showing a state as output.

One of the simplest examples of these would be a 1-dimensional cellular automaton in which each cell has two states, ON and OFF, which are represented by black and white, and where each cell turns on if at least one of its neighbors are in the ON state. When started from 1 cell, this simply creates a widening black line. When the layers are shown all at once, though, you can see that it makes a pyramidal shape.

All layers at once

For example, in the figure above, the second line is generated from doing the rule for all cells in the first line, the third line from the second line, and so on. More complicated figures can be generated from different rules, such as a cellular automaton in which a cell changes to ON if either the cell to it’s top left or top-right is ON, but not if both are on. This creates a Sierpinski Triangle when starting from a single cell:

Stephen Wolfram developed a numbering system for all cellular automata which base only on themselves, their left-hand neighbor, and their right-hand neighbor, often called the elementary cellular automata, which looks something like this for the Sierpinski Triangle automata (Rule 18):

This code has all possible ON and OFF states for three cells on the top, and the effect that it creates on the cell below them on the bottom. Using this system, we can find that there are 256 different elementary cellular automata. We can also easily create a number for each automaton by simply converting the ON and OFF states at the bottom to 1s and 0s, and then combining them to make a binary number (00010010 in the Sierpinski Triangle example). Then, we convert the binary to decimal and so get the rule number. (128*0+64*0+32*0+16*1+8*0+4*0+2*1+1*0= 18 for the example). We can also do the reverse to get a cellular automata from a number. Using this method, we can create pictures of all 255 elementary cellular automata:

Whilst some are rather boring, such as Rule 0, which is just white, or Rule 14, which is a single diagonal line.

There are many variations on this basic cellular automata type, such as an extension of the code where next-nearest neighbors are also included. This results in 4294967296 different cellular automata, a few of which appear to create almost 3-dimensional patterns such as the 3D Tetrahedrons cellular automata (rule 3283936144 ) which appears to show certain tetrahedral-ish shapes popping out of a plane.

There are also totalistic cellular automata, which are created by basing the next cell somehow on the average of the top-left, center, and top-right cells above it. These can have more than two states, and sometimes produce very strange-looking patterns, such as Rule 1599, a 3-state cellular automata:

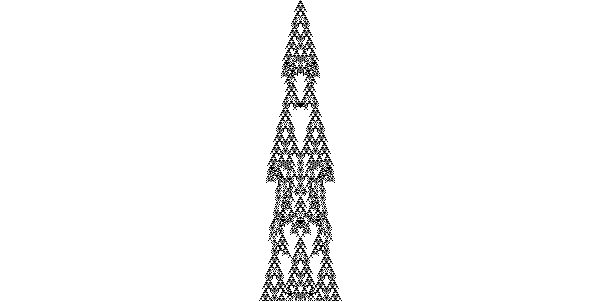
As well as all these, there are continuous-valued cellular automata, which, instead of having cells that can only be in certain states, have the cells have real-number values. Then, at every step a function is applied to the cell that is to be changed as well as it’s neighbors. A good example of this is the Heat cellular automaton, in which the function is ((left_neighbor+old_cell+right_neighbor)/3+ a number between 0 and 1) mod 1). It produces a “boiling” effect, in which it resembles a pot of water slowly boiling on an oven.

There are tons more 1-dimensional cellular automata; Stephen Wolfram filled most of an entire (1200 page) book with these. However, there are essentially only 4 classes of cellular automata. The first type is the most boring; it is where the cellular automata evolves into a single, uniform state. An example of this would be the Rule 254 elementary cellular automata (the first example), which eventually evolves into all black. The second type, repetition, is a little more interesting, as it does not evolve into a single state but is instead repetitive. This can include a single line, simple oscillation, or fractal-like behavior, an example of which would be Rule 18. The third type is simply completely chaotic behavior- not very interesting, but definitely more than the previous two- such as in Rule 30. The last type, type 4, is where there are many individual structures that interact, sometimes passing right through, other times blowing up. An example of this would be Rule 110. This type is probably the most interesting to watch, as the eventual outcome is unknown.